Scope
The following is based on Ray Toal's notes on scope in programming languages.
Definition
The scope of a binding is the region in a program in which the binding is active.
- Most languages employ static scoping (also called lexical scoping), meaning all scopes can be determined at compile time.
- Some languages (APL, Snobol, early LISP) employ dynamic scoping, meaning scopes depend on runtime execution.
- Perl lets you have both!
Regardless of whether scoping is static or dynamic, the definition implies that when you leave a scope, bindings are deactivated.
Static Scope
Static scoping is determined by the structure of the source code:
┌──────────────────────────────────────────────┐
procedure P │ (X: Integer) is │
┌─────────────┘ │
│ A, B: Integer; │
│ ┌────────────────────────────────────────┐ │
│ procedure Q │ (Y: Integer) is │ │
│ ┌─────────────┘ ┌───────────────────────────────────┐ │ │
│ │ function R │ (X, Y: Integer) return Integer is │ │ │
│ │ ┌────────────┘ ┌───────────────┐ │ │ │
│ │ │ procedure T │ is │ │ │ │
│ │ │ ┌─────────────┘ │ │ │ │
│ │ │ │ T: Integer; │ │ │ │
│ │ │ │ begin │ │ │ │
│ │ │ │ ... │ │ │ │
│ │ │ │ end T; │ │ │ │
│ │ │ └─────────────────────────────┘ │ │ │
│ │ │ W: Float; │ │ │
│ │ │ begin │ │ │
│ │ │ ... │ │ │
│ │ │ end R; │ │ │
│ │ └────────────────────────────────────────────────┘ │ │
│ │ ┌──────────────────────────────────┐ │ │
│ │ procedure S │ (Y: Integer) is │ │ │
│ │ ┌─────────────┘ │ │ │
│ │ │ begin │ │ │
│ │ │ ... │ │ │
│ │ │ end S; │ │ │
│ │ └────────────────────────────────────────────────┘ │ │
│ │ begin │ │
│ │ ... │ │
│ │ declare X: Integer; begin ... end; │ │
│ │ ... │ │
│ │ end Q; │ │
│ └──────────────────────────────────────────────────────┘ │
│ M: Integer; │
│ begin │
│ ... │
│ end P; │
└────────────────────────────────────────────────────────────┘
The general rule is that bindings are determined by finding the “innermost” declaration, searching outward through the enclosing scopes if needed.
Interestingly, not everything is obvious! There are reasonable questions regarding:
- Where exactly the scope of a particular binding begins and ends
- Whether bindings that have been hidden in inner scopes are still accessible
- What actually counts as a declaration versus just a use? Can declarations be implicit?
- The effect of redeclarations within a scope
Scope Range
Does the scope consist of a whole block or just from the declaration onward?
Consider this pseudocode:
var x = 3
var y = 5
function f() {
print y
var x = x + 1
var y = 7
print x
}
f()
Here is the the example translated into C code:
#include <stdio.h>
int x = 3;
int y = 5;
int main() {
printf("%d\n", y);
int x = x + 1;
int y = 7;
printf("%d\n", x);
}
main();
Here is what you get when you compile and run this code:
$ gcc foo.c foo.c:12:1: warning: type specifier missing, defaults to 'int' [-Wimplicit-int] main(); ^ 1 warning generated. $ ./a.out 5 2 $Is this what you expected? Hint: insert some additional local variables into the 'main' function and observe what happens.
Scope Holes
In static scoping, “inner” declarations hide, or shadow outer declarations of the same identifier, causing a hole in the scope of the outer identifier’s binding. But when we’re in the scope of the inner binding, can we still see the outer binding? Sometimes, we can:
In C++:
#include <iostream>
int x = 1;
namespace N {
int x = 2;
class C {
int x = 3;
void f() {
int x = 4;
std::cout << ::x; // global
std::cout << N::x; // namespace
std::cout << this->x; // class/object
std::cout << x; // function local
std::cout << '\n';
}
};
}
Here is code that works fine in C with the expected shadowing but will fail in Java:
void f()
{
int x = 1;
if (true) {
int x = 2;
}
}
Java does not allow more than one declaration of a local variable within a method.
JavaScript has a somewhat interesting take on the interplay of scopes and nested blocks, with very different semantics between declarations introduced with var, const, or let.
var and let in JavaScript, as it pertains to scope. You should run across something called the temporal dead zone (TDZ). Explain the TDZ in your own words.
Indicating Declarations
Generally, languages indicate declarations with a keyword, such as var, val, let, const, my, our, or def. Or sometimes we see a type name, as in:
int x = 5; // C, Java
or
X: Integer := 3; -- Ada
When we use these explicit declarations in a local scope, things are pretty easy to figure out, as in this JavaScript example:
let x = 1, y = 2;
function f() {
let x = 3; // local declaration
console.log(x); // uses local x
console.log(y); // uses global y, it’s automatically visible
}
f(); // writes 3 and 2
Easy to understand, for sure, but be super careful, leaving off the declaration keyword in JavaScript updates, and introduces if necessary, a global variable:
let x = 1;
function f() {
x = 2; // DID YOU FORGET let?
} // Updated global var! Accident or intentional?
f()
console.log(x);
Forgetting the declarating keywords has happened in the real world, with very sad consequences.
But in Python, there are no keywords and no types. Declarations are implicit. How does this work?
x = -5
def f():
print(abs(x))
f() # prints 5
Sure enough we
can see the globals abs and x inside
f. Now consider:
x = -5
def f():
x = 3
f()
print(x) # prints -5
Aha, so if we assign to a variable inside a function, that variable is implicitly declared to be a local variable. Now how about:
x = -5
def f():
print(x)
x = 3
f()
print(x)
This gives UnboundLocalError: local variable 'x' referenced
before assignment. The scope of the local x is the
whole function body!
Now Ruby’s declarations are also implicit. Let’s see what we can figure out here:
x = 3
def f(); puts x; end # Error!
f()
WHOA! NameError: undefined local variable or method `x' for main:Object. We can’t see that outer x inside of f! If we want to play this game, we must use global variables, which in Ruby start with a $:
$x = 3
def f(); x = 5; y = 4; p [$x, x, y] end # writes [3, 5, 4]
f()
So assigning to a local declares it, and variables starting with a $ are global.
CoffeeScript also has no explicit declarations. But it has a controversial design. If you assign to a variable inside a function, and that variable does not already have a binding in an outer scope, a new local variable is created. But if an outer binding does exist, you get an assignment to the outer variable.
x = 3
f = () -> x = 5
f() # Plasters the global x
console.log(x) # Writes 5
g = () -> y = 8
g() # Defines a local y which then goes away
console.log(y) # Throws ReferenceError: y is not defined
Redeclarations Within a Scope
If an identifier is redeclared within a scope, a language designer can choose to:
- Reject it (as a compile-time or run-time error).
- Make a fresh new binding and retain the old ones.
- Treat the redeclaration like an assignment.
Perl and ML actually retain the old bindings:
# Perl
my $x = 3; # declare $x and bind it
sub f {return $x + 5;} # uses the existing binding of $x
my $x = 2; # declare a NEW entity and thus a new binding
print f(), "\n";
(* SML *)
val x = 3; (* declare x and bind it *)
fun f() = x + 5; (* uses existing binding of x *)
val x = 2; (* declare a NEW entity and thus a new binding *)
f();
Both of these programs print 8, because the bindings are new:
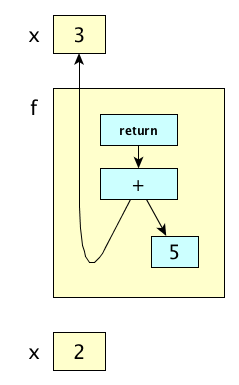
But in some languages, the second declaration is really just an assignment, rather than the creation of a new binding. In such a language, the code implementing the above example would print 7, not 8.
Dynamic Scope
With dynamic scoping, the current binding for a name is the one most recently encountered during execution. The following script prints 2, not 1:
# Perl
our $x = 1;
sub f{
print "$x\n";
}
sub g {
local $x = 2; # local makes dynamic scope (use my for static)
f();
}
g();
print "$x\n";
At each call, a new frame is created for each subroutine invocation and pushed on the call stack. A frame holds each of the locally declared variables for that invocation. In dynamic scoping, when looking up bindings for identifiers not in the current frame, we search the call stack. In our Perl example, while executing f and looking for $x, we’ll find it in g’s frame:
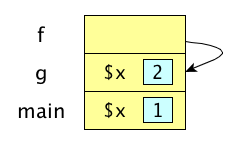
Dynamic scopes tend to require lots of runtime work: type checking, binding resolution, argument checking, etc.
They are also prone to redeclaration problems.
The principal argument in favor of dynamic scoping is the way they allow subroutines to be customized by using an “environment variable” style that allows selective overriding of a default (more or less). Michael Scott gives this example:
# Perl
our $print_base = 10;
sub print_integer {
...
# some code using $print_base
...
}
# So generally we want to use 10, but say at one point
# we were in a hex mood. We wrap the call in a block like this:
{
local $print_base = 16;
print_integer($n);
}
# At the end of the block the old value is essentially restored






