 |
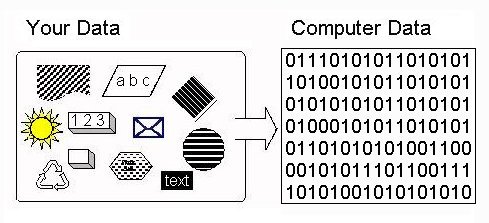
| Figure 1: Representing Real-World Data In The Computer |
 |
| Figure 1: Representing Real-World Data In The Computer |
Computers Are Electronic Machines. The computer uses electricity, not mechanical parts, for its data processing and storage. Electricity is plentiful, moves very fast through wires, and electrical parts fail less much less frequently than mechanical parts. The computer does have some mechanical parts, like its disk drive (which are often the sources for computer failures), but the internal data processing and storage is electronic, which is fast and reliable (as long as the computer is plugged in).
Electricity can flow through switches: if the switch is closed, the electricity flows; if the switch is open, the electricity does not flow. To process real-world data in the computer, we need a way to represent the data in switches. Computers do this representation using a binary coding system.
Binary and Switches.
Binary is a mathematical number system: a way of counting. We have all learned to
count using ten digits: 0-9. One probable reason is that we have ten fingers
to represent numbers. The computer has switches to represent data and switches
have only two states: ON and OFF. Binary has two digits to do the counting: 0 and 1 -
a natural fit to the two states of a switch (0 = OFF, 1 = ON).
As you can read about in the part of this course on the history of computers, the evolution of how switches were built made computers faster, cheaper, and smaller. Originally, a switch was a vacuum tube, about the size of a human thumb. In the 1950's the transistor was invented (and won its inventors a Noble Prize). It allowed a switch to be the size of a human finger nail. The development of integrated circuits in the 1960s allowed millions of transistors to be fabricated on a silicon chip - which allowed millions of switches on something the size of a finger nail.
Bits and Bytes
One binary digit (0 or 1) is referred to as a bit, which
is short for binary digit. Thus, one bit can
be implemented by one switch, as shown in Figure 2.
 |
| Figure 2 |
In the following table, we see that bits can be grouped together into larger chunks to represent data.
|
|
|
|
|
|
|
|
|
|
|
|
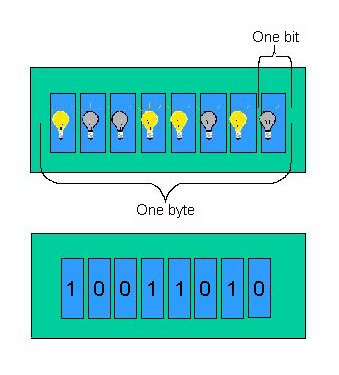 |
| Figure 3: Implementing a Byte |
Computer manufacturers express the capacity of memory and storage in terms of the number of bytes it can hold. The number of bytes can be expressed as kilobytes. Kilo represents 2 to the tenth power, or 1024. Kilobyte is abbreviated KB, or simply K. (Sometimes K is used casually to mean 1000, as in "I earned $30K last year.") A kilobyte is 1024 bytes. Thus, the memory of a 640K computer can store 640x1024, or 655,360 bytes. Memory capacity may also be expressed in terms of megabytes (1024x1024 bytes). One megabyte, abbreviated MB, means, roughly, one million bytes. With storage devices, manufacturers sometimes express memory amounts in terms of gigabytes (abbreviated GB); a gigabyte is roughly a billion bytes. Memory in older personal computers may hold only 640K bytes; in newer machines, memory may hold anywhere from 1MB to 32MB and more. Mainframe memories can hold gigabytes. Modern hard disks hold gigabytes.
|
|
Integers.
Integer numbers are represented by counting in binary.
Think for a minute how we count in decimal. We start with 0 and every new thing we count, we go to the next decimal digit. When we reach the end of the decimal digits (9), we use two digits to count by putting a digit in the "tens place" and then starting over again using our 10 digits. Thus, the decimal number 10 is a 1 in the "tens place" and a zero in the "ones place". Eleven is a 1 in the "tens place" and a 1 in the "ones place". And so on. If we need three digits, like 158, we use a third digit in the "hundred's place".
We do a similar thing to count in binary - except now we only have two digits: 0 and 1. So we start with 0, then 1, then we run out of digits, so we need to use two digits to keep counting. We do this by putting a 1 in the "two's place" and then using our two digits. Thus two is 10 binary: a 1 in the "two's place" and a 0 is the "one's place". Three is 11: a 1 in the "two's place" and a 1 in the "one's place". We ran out of digits again! Thus, four is 100: a one in the "four's place" a 0 in the "two's place" a 0 in the "one's place".
What "places" we use depends on the counting system. In our decimal system, which we call Base 10, we use powers of 10. Ten to the zero power is 1, so the counting starts in the "one's place". Ten to the one power is 10, so the counting continues in the "ten's place". Ten to the second power (10 squared) is 100, so we continue in the "hundred's place". And so on. Binary is Base 2. Thus, the "places" are two to the zero power ("one's place"), two to the one power ("two's place"), two to the second power ("four's place"), two to the third power ("eight's place"), and so on.
When you look at a byte, the rightmost bit is the "one's place". The next bit is the "two's place". The next the "four's place", The next the "eight's place" and so on. So, when we said that the byte:
|
|
|
|
The following table shows some binary counting:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
For some optional exercises and more detail on binary numbers, try the exercises at http://www.learnbinary.com (follow the tab links along the top of the banner.).
Characters.
The computer also uses a single byte to represent a single character.
But just what particular set of bits is
equivalent to which character? In theory we could each make up our own definitions, declaring certain bit
patterns to represent certain characters. Needless to say, this would be about as practical as each person
speaking his or her own special language. Since we need to communicate with the computer and with each
other, it is appropriate that we use a common scheme for data representation. That is, there must be
agreement on which groups of bits represent which characters.
The code called ASCII (pronounced "AS-key"), which stands for American Standard Code for Information Interchange, uses 7 bits for each character. Since there are exactly 128 unique combinations of 7 bits, this 7-bit code can represent only characters. A more common version is ASCII-8, also called extended ASCII, which uses 8 bits per character and can represent 256 different characters. For example, the letter A is represented by 01000001. The ASCII representation has been adopted as a standard by the U.S. government and is found in a variety of computers, particularly minicomputers and microcomputers. The following table shows part of the ASCII-8 code. Note that the byte:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
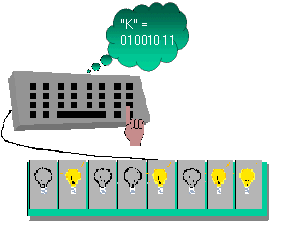
Thus, when you type a 'C' on the keyboard, circuitry on the keyboard and in the computer converts the 'C' to the byte:
|
|
 |
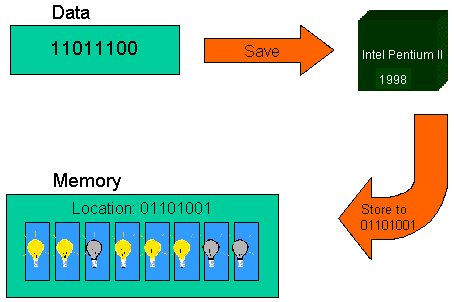 |
| Figure 4: Character As a Byte | Figure 5: Character Byte Stored In Memory |
|
| C |
|
| A |
|
| B |
Picture and Graphic Data.
You have probably seen photographs that have
been enlarged a lot, or shown close up - you can see that photographs are
a big grid of colored dots.
Computer graphic data like pictures, frames of a movie, drawings, or frames of an
animation are represented by a grid of pixels. "Pixel" is short for
picture element. In simple graphics (those without many
colors), a byte can represent a single pixel. In a graphic representation
called greyscale each pixel is a shade of grey from black at one
extreme to white at the other. Since eight bytes can hold 256 different integers
(0-255 as described a few paragraphs ago), a pixel in one byte can be one of 256 shades of
grey (usually with 0 being white and 255 being black). Modern video games and
colorful graphics use several bytes for each pixel (Nintendo 64 uses eight bytes = 64 bits
for each pixel to get a huge array of possible colors). A scanned photograph or
a computer drawing is thus stored as thousands of bytes - each byte, or
collection of bytes, representing a pixel. This is shown in Figure 6.
We saw that computer manufacturers got together and agreed how characters will be represented (the ASCII code). For graphics, there are several similar standards or formats. Two common picture formats used on the Internet are JPEG and GIF. These, like ASCII, are agreed-upon common coding of pixels in bytes.
| Figure 6: Graphics as a Collection of Pixel Bytes |
Sound Data As Bytes.
Sound occurs naturally as an analog wave, as shown in Figure 7.
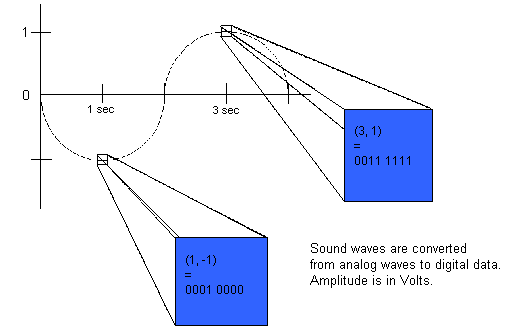 |
| Figure 7: Sound Data In Bytes |
To convert an analog wave into digital, converters use a process called sampling. They sample the height of the sound wave at regular intervals of time, often small fractions of a second. If one byte is used to hold a single sample of an analog wave, then the wave can be one of 256 different heights (0 being the lowest height and 255 being the highest). These heights represent the decibel level of the sound. Thus a spoken word might occupy several hundred bytes - each being a sample of the sound wave of the voice at a small fraction of a second. If these 100 bytes were sent to a computer's speaker, the spoken word would be reproduced.
Like ASCII for characters and GIF and JPEG for pictures, sound has several agreed-upon formats for representing samples in bytes. WAV is a common format on the Internet.
Program Data as Bytes.
When you buy a piece of software on a CD or diskette, you are getting a collection
of instructions that someone wrote to tell the computer to perform the task that
the software is meant to do. Each instruction is a byte, or a small collection
of bytes. If a computer used one byte for an instruction, it could have up to
256 instructions. Later we will look at what these instructions are, but for
now, you should realize that a byte could also be a computer's instruction.
The conversion of instructions to bytes is shown in Figure 8. The programming
process allows humans to write instructions in an English-like way. A
software program called a compiler then transforms the English-like
text into the bytes for instructions that the computer understands. This is
shown in Figure 9.
Like all other kinds of data, there are agreed-upon formats for computer instructions too. One reason that Macintosh computer programs do not run natively on PC-compatible (Intel-based) computers, is that Macintoshes and Intel PCs use different formats for coding instructions in bytes.
 |
| Figure 8: Instruction Data as a Byte |
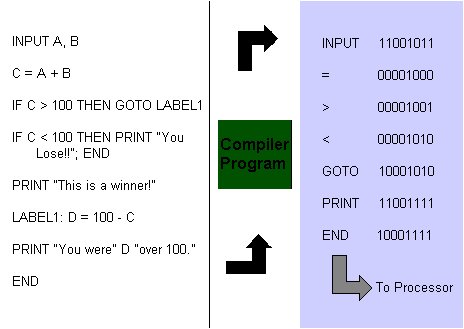 |
| Figure 9 |
|
|